Прежде всего, упростим наш анализ, ограничившись наиболее распространёнными типами первичных показателей. Будем предполагать, что исходный, первичный показатель — измерение — выполнено в непрерывной шкале (0, ∞). Такими являются выручка и некоторые натуральные показатели (выпуск продукции, время ремонта). Для оценки прибыли формально применяется шкала (–∞, ∞). Кроме того, в приведённых ниже практических примерах будем предполагать, что прибыль неотрицательна. Если компания оказалась в убытках, то отрицательному значению прибыли даётся нулевая оценка. Кроме того, введём ограничение, при котором нельзя делить отрицательный факт на отрицательный план, будем предполагать, что операция деления факт/план некорректна, если оба они отрицательны.
При делении фактического значения на плановое получается значение от нуля до очень больших величин. По какой шкале оценивать этот показатель? Иногда об этом не задумываются и просто используют в качестве оценки процент выполнения плана: (факт/план)×100%. Однако, это действие может привести к нежелательным управленческим последствиям. Каким? Покажем это на примере кусочно-линейной двухинтервальной шкалы, призванной демпфировать эти самые нежелательные управленческие последствия.
Кусочно-линейная двухинтервальная шкала
Кусочно-линейная двухинтервальная шкала — это шкала оценки полезности (ценности) показателя, которая задаёт его первичным значениям оценки в нескольких интервалах:
- если фактические значения показателя меньше Х% плана, то они имеют нулевую оценку — существенное невыполнение плана вознаграждения не заслуживает;
- если фактические значения показателя больше Х%, то далее до 100% идёт линейная шкала, заканчивающаяся оценкой 1 — небольшое недовыполнение плана вознаграждения всё же заслуживает;
- если фактические значения показателя больше 100%, то далее до Y% плана (Y% > 100%) идёт ещё одна линейная шкала, оканчивающаяся оценкой 2 (как правило) — перевыполнение плана стимулируется;
- если фактические значения показателя больше Y%, то все они тоже имеют оценку 2. Смысл в том, что столь значительное перевыполнение плана подозрительно, возможно, что план занижен, и потому больше 2-х премий за перевыполнение плана платить не следует.
Напомню, что общепринятых названий управленческим шкалам нет. Не нравится название кусочно-линейная двухинтервальная шкала? Пользуйтесь обозначением (Х, 100, Y) 1. В зарубежных проектах кусочно-линейная двухинтервальная шкала появилась довольно давно. У нас она появилась в 1990-х годах, но всё ещё только начинает приживаться.
Математическая формула кусочно-линейной двухинтервальной шкалы. Основание шкалы — это плановое значение показателя (100% плана). Значение оценки рассчитывается по формуле, где z — это фактическое значение показателя.
- Если x < z < 100% выполнения плана, то u(z) = (z – x)/(100% – x), u(z) = 0 при x ≥ z;
- Если y > z > 100% выполнения плана, то u(z) = (z – 100%)/(y – 100%), u(z) = 2 при y ≤ z.
Пример кусочно-линейной двухинтервальной шкалы показан на рисунке 2. Значение оценки находится в интервале [0; 2]. Различные отрезки (интервалы) шкалы выполняют разные роли:
- (0, Х) – отсутствие стимулирования выполнения плана ниже определенной нижней границы, меньшей 100 %;
- (Х, 100) – стимулирование выполнения плана после достижения минимально приемлемого результата плюс защита от завышенного плана;
- (100, Y) – стимулирование перевыполнения плана, но в определенных пределах;
- (Y, бесконечность) – бюджетирование и защита от заниженного плана.
Преимущества и недостатки кусочно-линейной двухинтервальной шкалы. Эта шкала является наиболее общей из непрерывных шкал при оценке степени достижения плана и чаще всего применяется в системах вознаграждения. Она сглаживает недостатки многих частных шкал, и тем, кто работал с ней, трудно без нее обойтись. Руководителю она удобна для мотивации сотрудников: «Я готов учесть каждый процент приближения к плану, чтобы не допустить демотивации сотрудников и выжать из них все, что можно».
Пример. Наиболее популярный вариант шкалы (Х, 100, Y) — это (80, 100, 130), где интервалы располагаются между значениями 80%, 100% и 130% выполнения плана соответственно. Рассмотрим эту шкалу подробнее (рис. 2).
Нижняя граница — 80% плана. Начальники будут стремиться завысить план, и потому несправедливо полностью лишать исполнителей бонуса при небольшом недовыполнении плана.
Верхняя граница — 130% плана. Это ограничение действует в случае, если план оказался заниженным. Лёгкость перевыполнения заниженного плана на 200 или 300% не должна позволить менеджеру получить незаслуженно высокий бонус.
За 80% плана или того меньше ещё нет бонуса, то есть локальная функция полезности равна нулю. За 100% плана начисляется один бонус, а за 130% — два бонуса. Удвоение бонуса — это максимум, на который может рассчитывать исполнитель. В интервалах от 80 до 100% и от 100 до 130% бонусы растут линейно в зависимости от фактически достигнутого значения показателя 2.
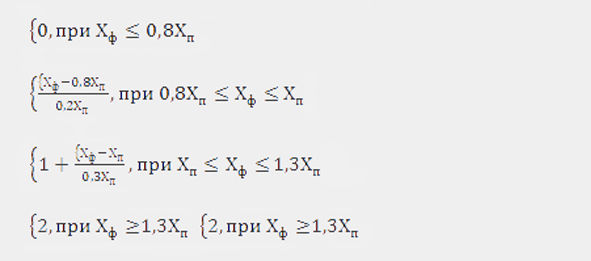
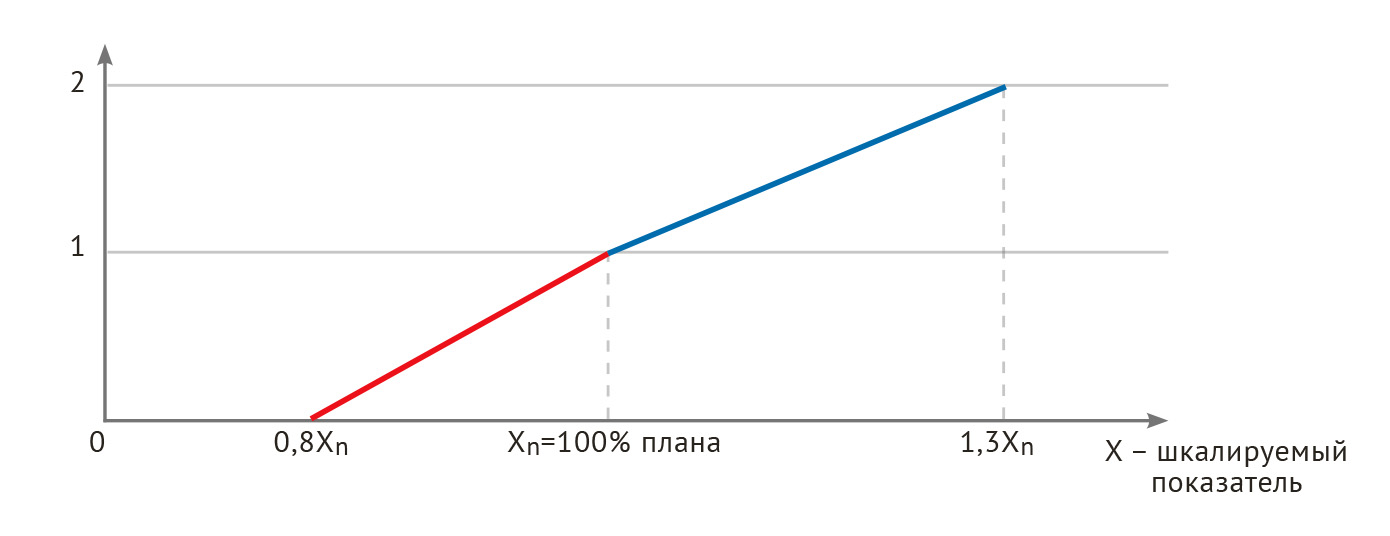
Рис. 2. График кусочно-линейной двухинтервальной шкалы (80, 100, 130)
Сама по себе кусочно-линейная двухинтервальная шкала не плоха и не хороша — всё зависит от контекста её использования. И конечно, её границы могут быть изменены, и вместо базового варианта шкалы (80, 100, 130) можно, например, применить (60, 100, 120) или другие варианты. Причём для разных показателей можно и нужно назначать разные варианты этой шкалы. С одной стороны это затрудняет использование шкалы (Х, 100, Y) на практике, с другой повышает точность. В частности, в одной крупной компании в 2005 году сквозное использование базового варианта шкалы (80, 100, 130) явилось одной из причин неудачного внедрения системы сбалансированных показателей. Вместе с тем, шкалу (Х, 100, Y) нельзя считать пригодной на все случаи жизни. Варианты использования иных шкал — успешные и не очень — мы рассмотрим ниже.
Использование шкалы (Х, 100, Y) на практике
Как можно использовать такую шкалу, например, для свёртки двух KPI в один комплексный показатель? Алгоритм таков:- шаг 1 — назначение плановых значений для каждого KPI;
- шаг 2 — шкалирование показателей, допустим, для первого показателя выбрана шкала (80, 100, 130), а для второго — (70, 100, 150);
- шаг 3 — присвоение весов показателей, допустим, 40% и 60% (в формуле будут использованы доли 0,4 и 0,6, соответственно).
- оценка (локальная функция полезности) первого показателя: (90 – 80)/20 = 0,5;
- оценка второго показателя: 1 + (105 – 100)/50 = 1,1%
- общая функция полезности (комплексная) будет равна: 0,4×0,5 + 0,6×1,1 = 0,86.
Для оцифровки показателя по шкале (X, 100, Y) необходимо учесть четыре точки:
- плановое значение (выполнение плана на 100%), в идеале оно устанавливается в процессе бюджетирования; если значение не задано бюджетом, его требуется рассчитать или определить экспертно;
- фактическое значение (точка Z) — результат деятельности за прошедший период;
- минимальное пороговое значение (точка X) — критическая точка, отражающая минимальное допустимое выполнение плана, сверх которого имеет смысл учитывать результат деятельности как положительный;
- максимальное пороговое значение (точка Y) — критическая точка, отражающая максимальное возможное перевыполнение плана и далее перевыполнение плана не учитывается.
Дискретные шкалы
Существует два основных типа дискретных шкал: одноуровневые и многоуровневые.
Дискретная одноуровневая шкала принимает два значения:
- 1 — план выполнен или перевыполнен;
- 0 — план не выполнен.
Это шкала в стиле «всё или ничего», никаких компромиссов (рис. 3).
Математическая формула дискретной одноуровневой шкалы очевидна:
u(x) = 1 при Х лучше Хпл,
u(x) = 0 при Х хуже Хпл.
Преимущества и недостатки дискретной одноуровневой шкалы. Такая шкала очень проста с точки зрения руководителя: «Мне нужно, чтобы они выполнили план, и всё. Какие ещё шкалы оценки степени приближения к плану? Не выполнят — ничего не получат». Такая точка зрения популярна и часто оправдана, однако и недостатков у неё хватает.
Во-первых, эта шкала не стимулирует непрерывность улучшений. Во-вторых, она совсем не гибкая, это своеобразный „грубый пинок”. Поэтому при использовании такой шкалы возможен обратный эффект — демотивация сотрудников. Зачем перевыполнять план? Такая мысль придёт наверняка в голову любому сотруднику, действия которого оцениваются шкалой (0 или 1).
Дискретная многоуровневая шкала принимает несколько значений в зависимости от степени достижения части, ступеньки целевого значения показателя, например, 40%, 60%, 80% (рис. 4). Например, в одном банке использовалась следующая пятибалльная шкала оценки степени реализации проектов:
Оценка u(x) = 5, если процент успешной реализации = 100;
4, если процент успешной реализации >80 и <100;
3, если процент успешной реализации >60 и ≤80;
2, если процент успешной реализации >40 и ≤60;
1, если процент успешной реализации >20 и ≤40;
0, если процент успешной реализации ≤20.
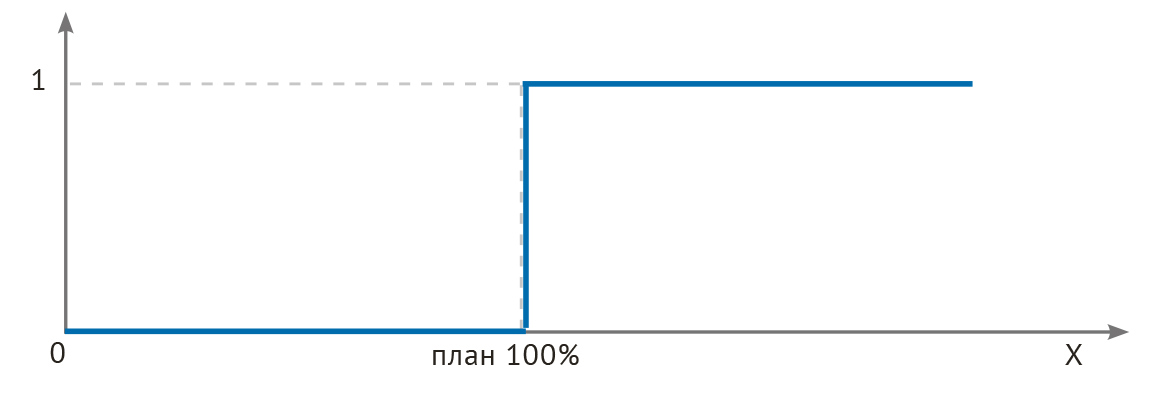
Рис. 3. Оценка показателя с помощью дискретной одноуровневой шкалы: «всё или ничего».
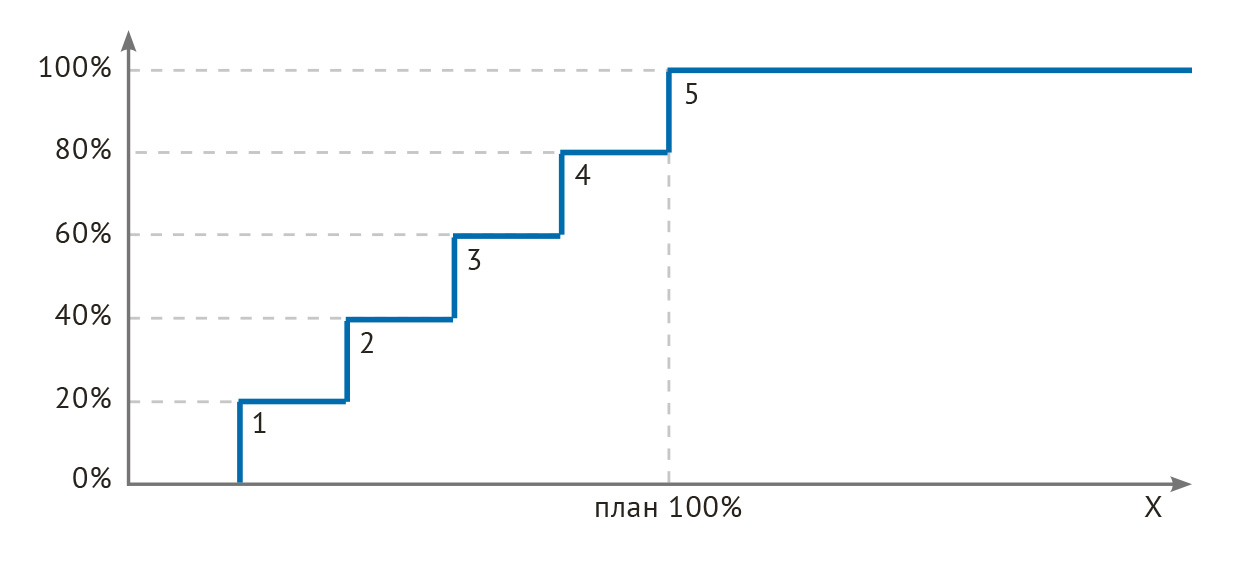
Рис. 4. Пример оценки показателя факт/план с помощью дискретной многоуровневой шкалы.
Преимущества и недостатки дискретной двухуровневой шкалы. С точки зрения руководителя цель такой шкалы понятна — заставить сотрудников карабкаться на новый уровень, а промежуточные результаты не в счёт. «Мне нужно, чтобы сотрудники выполнили план. Но поскольку план, возможно, завышен, я готов смягчить требования, чтобы не допустить демотивации работников. Пусть хоть часть сделают. Они пошагово движутся к идеалу, и это поощряется».
Однако, эта шкала не стимулирует непрерывность улучшений. Поэтому возможна демотивация сотрудников, причём именно из-за используемой шкалы. Примером относительно удачного применения шкалы можно назвать оценку успешности реализации проектов. В проектах чаще всего работы и этапы надо выполнить до конца и сдать. И в такой ситуации использование дискретной многоуровневой шкалы будет достаточно адекватным.
Обращаю ваше внимание, что не совсем корректно говорить, что одна шкала лучше другой. Одна шкала будет актуальнее и полезнее, чем другая лишь в определённой ситуации.
Пример использования многоинтервальной и смешанной шкал
В одной медицинской компании использовались два вида шкал. Первая шкала — дискретная многоинтервальная, использовалась для расчёта KPI обеспечивающих структурных подразделений (рис. 5). Премия по KPI не рассчитывается при фактическом выполнении плана менее чем на 80% от плана.Формула этой дискретной многоинтервальной шкалы:
- план выполнен на 80 — 89,9% — оценка 0,8;
- план выполнен на 90 — 99,9% — оценка 0,9;
- план выполнен на 100% — 1;
- план выполнен на 101 — 120% — плюс по 0,02 за каждые 5% перевыполнения;
- план выполнен на 120% и выше — оценка 1.
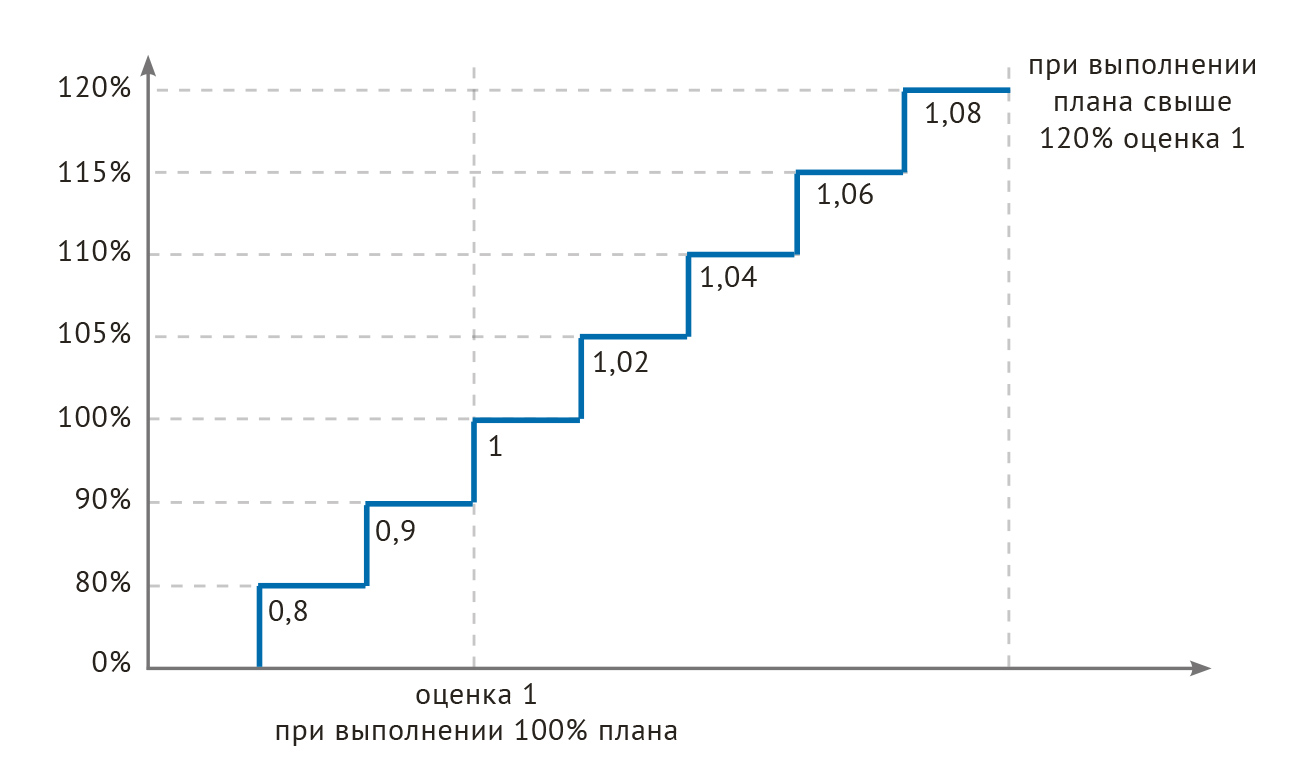
Рис. 5. Дискретная многоинтервальная шкала рассчёта KPI для обеспечивающих структурных подразделений (измерение фактического результата — по вертикали, а его оценка — по горизонтали).
Вторая шкала использовалась для рассчёта KPI по коммерческим структурным подразделениям (рис. 6). Это была уже смешанная шкала, частично дискретная, а частично — линейная. Здесь премия по KPI не рассчитывалась при выполнении меньше 90% плана. Формула этой частично дискретной, а частично линейной шкалы:
- план выполнен на 90 — 99,9% — оценка 0,9 — 0,999 (это непрерывно-линейный участок шкалы);план выполнен на 100 — 120% — оценка 1,1;план выполнен на 120% и выше — оценка 1,2.
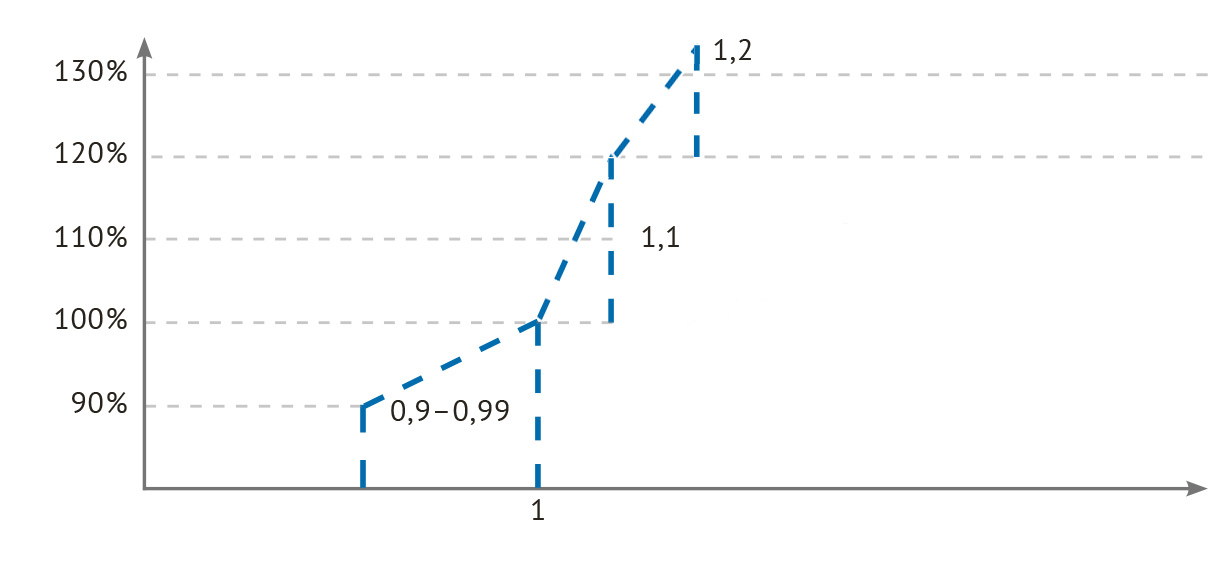
Рис. 6. Частично дискретная и частично линейная шкала рассчёта KPI для коммерческих структурных подразделений (измерение фактического результата — по вертикали, а его оценка — по горизонтали).
* * *
В следующей части цикла мы поговорим об экзотических шкалах.






Чтобы оставить комментарий пожалуйста Авторизуйтесь