Управленческая теория измерений.

Есть ложь, есть наглая ложь и есть статистика.
Марк Твен

Различные измерения и показатели используются в каждой фирме, в любой организации. Выбор подходов к оценке степени достижения некоторого показателя (например, плана продаж) огромен. Задача этой статьи — не придумывать что-то своё, а попытаться классифицировать доминирующее большинство существующих подходов к измерению показателей.
Обработка результатов измерений используется для получения выводов. Хорошая обработка результатов измерений — это достоверная система оценок (термин квалиметрии, принятый нами на вооружение). Увы, мой опыт показывает, что менеджеры часто не замечают явных логических нестыковок. Причина очевидна: не хватает специальной математической подготовки и экономических знаний. Поэтому в этой части статьи мы проанализируем наиболее распространённые ошибки.

Какие средние можно использовать для измерений по порядковым шкалам?

Ошибки при выводах, сделанных на основе средних величин, в порядковых шкалах случались не раз. В спорте, в социологии, в психологии они известны (примеры смотрите ниже). В менеджменте они тоже случаются, просто не публикуются и потому не обсуждаются. То, что со средними величинами для анализа измерений по порядковым шкалам надо быть очень аккуратным, показывает врезка «Средний балл не всегда показывает однозначно, кто лучше учится».

Теория измерений выносит жёсткий приговор среднему арифметическому: использовать его для анализа измерений в порядковой шкале нельзя.

Заметим, что если один набор измерений „лежит над другим”, то это означает, что эксперты полностью согласны между собой. Например, из двух оцениваемых объектов один лучше для всех экспертов. Тогда и среднее не нужно, всё и так ясно: первый объект лучше.

Однако в любой более сложной ситуации обычные средние, кроме моды и медианы, могут вызывать ошибки (см. врезку «Если средний балл больше, то это не значит, что объект измерений лучше!»). А именно в такой ситуации и нужны статистики для выводов. В частности, такие ситуации нередки в системе показателей деятельности компании .

Однако те, кто не знает теории измерений, постоянно используют среднее арифметическое для измерений по порядковым шкалам. Всегда ли они ошибаются? Точнее, в каких случаях среднее арифметическое коварно и может привести к ошибке? А когда оно безобидно? Оказывается, можно в какой-то мере реабилитировать среднее арифметическое, если перейти к вероятностной постановке и удовлетвориться результатами для больших объёмов выборок [2].

Если средний балл больше, то это не значит, что объект измерений лучше!

Результаты измерений в порядковых шкалах должны интерпретироваться не так, как мы привыкли. В книге [2] приводится социологическое исследование, послужившее поводом к развитию одного из направлений отечественных исследований по теории измерений. При изучении привлекательности различных профессий для выпускников новосибирских школ был составлен список из 30 профессий. Опрашиваемых просили оценить каждую из этих профессий одним из баллов 1, 2,..., 10 по правилу: чем больше нравится, тем выше балл .
Для получения социологических выводов необходимо было дать единую оценку привлекательности определённой профессии для совокупности выпускников школ. В качестве такой оценки использовалось среднее арифметическое баллов, выставленных профессии опрошенными школьниками. Заметим, что так обычно и поступают люди, не знакомые с теорией измерений. В частности, физика получила средний балл 7,69, а математика — 7,50. Поскольку 7,69 больше, чем 7,50, был сделан вывод, что физика более предпочтительна для школьников, чем математика. Однако этот вывод противоречит данным другого исследования, согласно которым ленинградские (дело было в СССР) школьники средних классов больше любят математику, чем физику.
Как объяснить это противоречие? Есть много подходов к выяснению причин различия выводов новосибирских и ленинградских исследователей. Одно из возможных объяснений этого противоречия основано на теории измерений. С точки зрения теории измерений обработка статистических порядковых данных о предпочтениях выпускников школ с помощью среднего арифметического неверна.
Дело в том, что баллы 1, 2,..., 10 введены конкретными исследователями, то есть субъективно. Если одна дисциплина оценена в 10 баллов, а вторая — в 2, то из этого нельзя заключить, что первая ровно в 5 раз привлекательней второй. Другой коллектив социологов мог бы принять иную систему баллов, например, «школьную» (1, 2, 3, 4, 5), и тогда «дистанция» между оценками профессий, а также средняя оценка дисциплин очевидно изменились бы. Естественно предположить, что упорядочивание профессий по привлекательности, присущее школьникам, не должно зависеть от того, какой системой баллов им предложит пользоваться социолог. Это лишний раз подтверждает вывод об ошибочности использования среднего арифметического (а также среднего геометрического, гармонического и квадратичного) для анализа результатов этих измерений.

Врезка «Выбор порядковой шкалы влияет на выводы, получаемые по средним оценкам» показывает, что проблема адекватности измерений может быть важной для построения системы показателей. Хотя эта проблема явно и не основная. Тем не менее, надо понять, какие статистические показатели измерений по порядковым шкалам будут корректными для использования в системе показателей.

Итак, средним арифметическим в порядковой шкале пользоваться нельзя. Чем же заменить среднее арифметическое в качестве адекватной меры среднего значения измерений в порядковых шкалах? Медиана в качестве среднего даёт удовлетворительную оценку. Эта оценка не смещается при выборе разных видов порядковой шкалы. Это значит, что «медианный показатель» при любой шкале один и тот же. В этом плюс медианы. В примере во врезке «Выбор порядковой шкалы влияет на выводы, получаемые по средним оценкам» при любых порядковых шкалах медиана — оценка «удовлетворительно». Понятно, что минусы у медианы тоже есть. Но, по крайней мере, она не смещается при пересмотре шкал. Поэтому медиану математики рекомендуют в качестве среднего при измерениях по порядковым шкалам.

Выбор порядковой шкалы влияет на выводы, получаемые по средним оценкам

Кому не известна пятибалльная шкала? И все знают один её недостаток: единицей в школе практически не пользуются. А насколько достоверны измерения по такой шкале? И что будет, если немного изменить порядковую шкалу? Попробуем разобраться.
Рассмотрим три порядковые балльные шкалы:

• обычную «школьную» шкалу: 2, 3, 4, 5 — «неуд.», «уд.», «хор.», «отл.»;
• скорректированную «школьную» шкалу: 1, 3, 4, 5 — «неуд.», «уд.», «хор.», «отл.» (один учитель предложил исправить обычную «школьную» шкалу, введя оценку 1 за неудовлетворительные знания);
• модифицированную «школьную» шкалу: 0, 3, 4, 5 — «неуд.», «уд.», «хор.», «отл.» (другой учитель считает, что неудовлетворительные знания эквивалентны отсутствию знаний и потому предложил использовать такую шкалу).

Предположим, школьник получил 3 оценки: «неуд.», «уд.», «хор.».
Средняя оценка по первой шкале: 3. Вывод: в среднем ученик учится на «удовлетворительно». Это не очень правильный вывод. Ведь по одному из предметов наш школьник не удовлетворил требованиям — получил «неуд», а средняя оценка это скрыла.
Средняя оценка по второй шкале: 2,67. Вывод: в среднем ученик учится в интервале от «неудовлетворительно» до «удовлетворительно», но ближе к «удовлетворительно». Вам нравится такой вывод?
Средняя оценка по третьей шкале: 2,33. Вывод: в среднем ученик учится в интервале от «неудовлетворительно» до «удовлетворительно», но ближе к «неудовлетворительно». Итак, по одним и тем же простейшим данным, заданным в порядковой шкале, мы получили три варианта вывода. То есть:
Использование среднего арифметического в порядковых шкалах приводит к ошибкам. Выбор порядковой шкалы влияет на выводы, получаемые по средним оценкам.
Возражение практика: мы всегда используем одну и ту же обычную шкалу. Поэтому все выводы стандартизированы и в любой школе в описанной ситуации вывод будет одинаковым. И это хорошо.
Доводы эксперта — отлично, что выводы одинаковы, однако:

• при построении системы показателей мы сами выбираем шкалы. Поэтому в одной фирме (в один момент времени на одной и той же фирме) используется одна шкала, в другой фирме (в другой момент времени на одной и той же фирме) применяют иную шкалу. Ситуации на фирмах могут быть одинаковы, а выводы разными;
• даже при использовании общепринятых шкал выводы могут быть некорректными. Пример: в приведённом примере мнения учителей о шкале были разными.

Справедливости ради отметим, что не только медианами оцениваются измерения по порядковым шкалам. Меры близости в порядковых шкалах оцениваются разными коэффициентами корреляции. Термин «корреляция» означает «связь». Допустимые меры близости в порядковых шкалах должны быть инвариантными относительно допустимых преобразований порядковой шкалы, то есть остаются постоянными при любом строго возрастающем преобразовании шкалы измерения результатов наблюдений. Самой популярной мерой близости в порядковых шкалах является коэффициент ранговой корреляции Спирмена, который определяет степень близости между двумя ранжировками.

Есть и другие коэффициенты корреляции. Самый известный из них — коэффициент тау Кендалла для ранговой корреляции. Но оценка корреляции в системе показателей компании — это баловство. Мне неизвестны примеры, когда использование коэффициентов корреляции было бы критически важно. Поэтому мы не будем рассматривать коэффициенты корреляции.

Какие средние можно использовать для измерений по количественным шкалам?

В количественных шкалах осмысленными и допустимыми являются действия сложения и вычитания. Казалось бы, ситуация тут привычная и понятная, можно использовать все средние величины. Однако традиция использования среднего арифметического может приводить к экономически ошибочным выводам. Причина — неравномерность распределения результатов по шкале.

Пример. Пусть 5 работников имеют такие зарплаты в у. е.: 100, 100, 200, 500, 600. Для этих показателей имеем три средние величины: моду (100 у. е.), медиану (200 у. е.) и среднее арифметическое (300 у. е.). Они разные, и какое из них правильно использовать как показатель зарплаты всей группы работников? Ответ «среднее арифметическое», который дают многие, неверен.

Доход выше среднего арифметического доступен немногим. Это объясняется наличием очень богатых людей (пусть и немногих), которые сильно влияют на среднее арифметическое. Показатель среднего арифметического доходов всех людей очень чувствителен к увеличению или уменьшению доли высокодоходных или низкодоходных групп населения. Это хорошо показано во врезках «Марш карандашей» и «Сравнение оценок среднего дохода».

Марш карандашей

Для того чтобы лучше понять и ощутить, как правильно описывать распределение дохода, используют аналогию голландского профессора Пена (Pen's analogy), в которой каждый человек представлен своим доходом в виде карандаша . Чем больше доход, тем больше карандаш. Если мы примем, что «средний человек» — это целый карандаш, тогда «медианный человек» — это совсем небольшой карандашик.
Мысленно устроим «парад карандашей», допустим, в течение часа. Сначала пойдут самые маленькие карандашики и первые 2 — 3 минуты вам будет трудно их рассмотреть, через пять минут они вырастут до размеров сигаретного фильтра. В течение следующих 25 минут идут, постепенно увеличиваясь, небольшие карандашики, шествие которых оканчивается «медианным человеком» (то есть прошла ровно половина). Следующие 20 минут долго и нудно проходят карандаши размером от половины до почти целого, и только за 10 минут до конца парада появляется «средний человек» — целый карандаш. После этого картина быстро меняется. Появляются всё более и более длинные карандаши: сначала юристы примерно по 18 футов, затем высококвалифицированные медики и ведущие бухгалтеры длиной от 7 до 8 ярдов и управляющие по 20 и более ярдов. И, наконец, пройдёт Поль Гетти — самый богатый в то время человек — «длиной в 20 миль».
Таким образом, мы видим, что оценка «средний человек» почти ничего не говорит о характере распределения доходов.

Математически средний доход можно вычислить разными методами. Это и среднее арифметическое, и мода, то есть интервал с наибольшим представительством, или медиана, меньше и больше которой лежит половина значений. Но экономически корректнее медиана. Слева от «медианного дохода» лежат значения доходов 50% людей и справа от «медианного заработка» лежат 50%. «Медианный доход» наиболее точен с экономической точки зрения для оценки среднего заработка (см. врезку «Сравнение оценок среднего дохода»). Именно поэтому в статистике доходов большинства развитых стран для характеристики среднего и, соответственно, общего уровня доходов приводится не средний, а медианный их уровень, то есть уровень, выше и ниже которого получает доход одинаковое число семей.

Сравнение оценок среднего дохода

Среднее арифметическое значение дохода завышено за счёт наличия очень богатых людей.
Пример. Допустим в 2000 году 11 человек еле-еле сводили концы с концами, зарабатывая по 3000 руб. в месяц, а один «выбился в люди» — его месячный доход составляет 147 000 руб. Средняя зарплата этой группы высокая — 15 000 руб., что значительно выше прожиточного минимума в то время.
Зачем используется подобная статистика? Для того чтобы, опираясь на неё, маркетологи могли давать дельные советы. Теперь представьте себе коммерсанта, ориентирующегося на среднюю зарплату. Его товары, рассчитанные на «средний класс», не найдут сбыта среди наших 11 человек, так как одним они не по карману, а другим не нужны. Очевидно, что за оценку средней зарплаты следует принять 3000 руб. (а это и есть медиана), и тогда коммерсант не промахнётся.
Мода тоже плохо отражает распределение заработка. Модой в нашем случае называют интервал, в который попало больше всего людей. За счёт произвольности выбора деления на интервалы мода сильно меняется. При таком выборе больше влияние случая, в том числе за счёт «двугорбых» распределений зарплаты, столь характерных в условиях размывания среднего класса в России. Допустим, что имеется следующее распределение годового заработка:

Мода по этим данным даёт неточный результат — 300 000 руб., смещая среднюю оценку в нижнюю точку. При этом существование второго «горба», ближе к 700 000, игнорируется.
Медиана даёт экономически наиболее точный результат. В нашем примере всего указаны доходы 61 человека. «Медианный человек» — 31-й по порядку снизу вверх, у него годовой доход 500 000 руб. Это гораздо корректнее отражает заработок группы.

Интересно, что для наблюдающихся в реальной жизни распределений доходов и заработной платы справедлива следующая закономерность: мода меньше медианы, а медиана меньше среднего арифметического (см. врезку «Распределение заработка — зависимость, которую не удаётся объяснить»).

Значение математической теории измерений

Итак, мы видим, что для каждого показателя есть своё корректное среднее. Например, для инфляции настоящее «среднее» — это среднее геометрическое, для средней зарплаты в компании — это медиана, для курса доллара на бирже — это средневзвешенное.

Приведённые выше выводы, касающиеся средних величин, широко применяются, причём не только в экономике, менеджменте, теории экспертных оценок или социологии, но и в инженерном деле, например, для анализа методов агрегирования датчиков в АСУ ТП доменных печей. Велико прикладное значение теории измерений в задачах стандартизации и управления качеством.

Распределение заработка — зависимость, которую не удаётся объяснить

Экономическая наука состоит из теоретических законов,
которые никто не может верифицировать, и эмпирических
законов, которые никто не может объяснить.
М. Калецки

Распределение заработка даёт прекрасный пример зависимости, которую никто не может объяснить. Оно показывает долю тех, кто зарабатывает в единицу времени (как правило, за год) известное количество денег. При этом измеряют не точную денежную сумму, а её попадание в небольшой интервал.
Оказывается, распределение заработка по группам населения почти не зависит от страны, региона, времени и других очень существенных факторов. Казалось бы, этого не может быть. Но тем не менее, это так.
Для наглядности будем описывать распределение непрерывной функцией распределения. С экономико-математической точки зрения наиболее точно типичное распределение заработка описывается кривой распределения, показанной на рисунке, сглаженной с правой стороны (окончание кривой получило название «парето-хвост», по имени итальянского экономиста Вильфредо Парето).

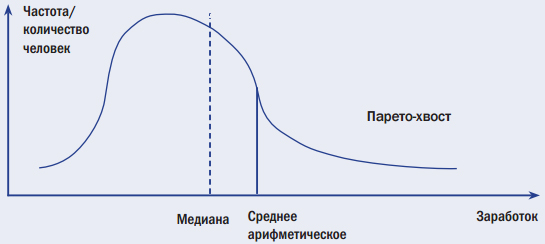
Рис. 1. Типичная кривая распределения заработка.

Казалось бы, в разные времена и в разных странах могут быть самые разнообразные распределения заработка. Но... фантастика! Если привести все распределения к одной (относительной) системе координат, то окажется, что распределение практически едино для всех времен и народов.

Теория измерений способна дать практические рекомендации:

• по выбору шкал измерений;
• по выбору адекватных статистических показателей и различного рода средних для агрегирования информации и сопоставления результатов измерений;
• по определению сравнительной достоверности и информативности измерений, привести к выбору шкал с нужными параметрами достоверности и информативности.

Последним мы и займемся в следующей статье.

1. Орлов А. И. Устойчивость в социально-экономических моделях. — М.: Наука, 1979. — 296 с.
2. Орлов А. И. Нечисловая статистика. — М.: МЗ-Пресс, 2004.
3. Пфанцагль И. Теория измерений/ Пер. с нем. — М.: Мир, 1976. — 165 с.
4. Фишберн П. Измерение относительных ценностей. — в кн.: Статистическое измерение качественных характеристик. —ика, 1972, — с. 35 — 94.

Комментарии 0