Управленческие шкалы.

Измерения и оценки в задачах управления

Принятие решений немыслимо без измерения и оценки разнородных фактов и данных. Поэтому одна из задач менеджмента — выстроить числовую систему показателей, которая позволит выразить всё необходимое для оценки, мотивации и принятия решений, через конкретные бизнес-показатели. Это совсем не означает, что мы пытаемся всё формализовать, субъективные оценки ещё никто не отменял, но они тоже должны стать частью управленческой теории измерений.

К сожалению, теория измерений и квалиметрия [3, 6 — 12] оказались слишком общими для массового применения в менеджменте. Иначе бы полезные приёмы и формулы быстро распространились в жадной до всего практичного сфере менеджмента. Поэтому возникла задача создания управленческой теории измерений, о которой я рассказал в цикле «Управленческая теория измерений».

Измерения и оценки показателей — это ключевые понятия, причём это разные понятия 1. Шкалам, используемым для оценки показателей, и посвящён настоящий цикл, именно их я и называю управленческими шкалами. Здесь мы будем рассматривать шкалирование только частных показателей, об интегральных и комплексных показателях надо рассказывать отдельно.

Надо отметить, что системы показателей для мотивации, оценки качества управления и оценки бизнеса, вообще говоря, отличаются, хотя различий в них немного. Чтобы упростить рассказ об управленческих шкалах, ниже я опишу подходы к оценке показателей (то есть к шкалированию, см. врезку) в основном в целях мотивации и вознаграждения сотрудников, так как это самая популярная область применения.

Проблема выбора шкал

Выбор подхода к оценке степени достижения целевых значений показателей (например, плана продаж) зависит от ситуаций, вида работ, конкретной фирмы и т. д. Но принципиальных подходов немного, их можно классифицировать и описать математически.

Выбор типа шкалы зависит от:

• самого показателя и целей его применения;
• шкалы измерений, то есть от шкалы первичного показателя;
• значений показателя: плановых и фактических, нормативных и граничных.

Очевидно, что шкала исходных измерений оказывает существенное влияние на выбор оценочных шкал. Выбора шкал не так очевиден, как это может показаться на первый взгляд, проблема выбора проиллюстрирована во врезке «Пример неоднозначности перевода в проценты».

Важно понимать, что выбор подхода к оценке степени достижения целевого значения показателя зависит от того, с какой целью выполняется оценка. На мой взгляд, существует лишь три направления использования управленческой теории измерений: оценка, мотивация и решения. Последнее направление отлично обобщено в книге Филинова-Чернышева [14, с. 118 — 127]. В ней разделены инструментальные и экспертные показатели, для первых есть аппарат (прибор, прямой счёт, формула, алгоритм и т. д.), а для вторых только экспертное суждение. Шкала инструментального показателя, как правило, уже задана и измерение очевидно, а для экспертного показателя первичную шкалу ещё надо предложить.

Число применяемых шкал и приёмов шкалирования велико. Далее я подробно остановлюсь как на хорошо известных шкалах теории измерений, так и на разработанных с учётом особенностей компаний и задач в рамках консультационных проектов.

Одноинтервальные шкалы: линейная и нелинейная

Линейная одноинтервальная шкала — это шкала оценки полезности (ценности) показателя, которая даёт его первичным значениям оценки в интервале (0, 1), и именно поэтому иногда обозначается (0, 1) (рис. 1). Также она называется «максиминной» линейной шкалой. Это одна из самых популярных шкал оценки значений показателей без планового значения.

Математическая формула линейной одноинтервальной шкалы. Для возрастающих по полезности показателей (чем больше значение, тем лучше) используется формула:

u(x) = (x – x_min)/(x_max – x_min), 0 ≤ u(x) ≤ 1; u(x) = 1 при х_max ≤ х и u(x) = 0 при х ≤ х_min (1),

где:
х — значение показателя (фактическое, плановое, целевое);
х_min — минимальное значение „рабочего” интервала, это худшее значение возрастающего по полезности показателя;
х_max — лучшее значение возрастающего по полезности показателя.

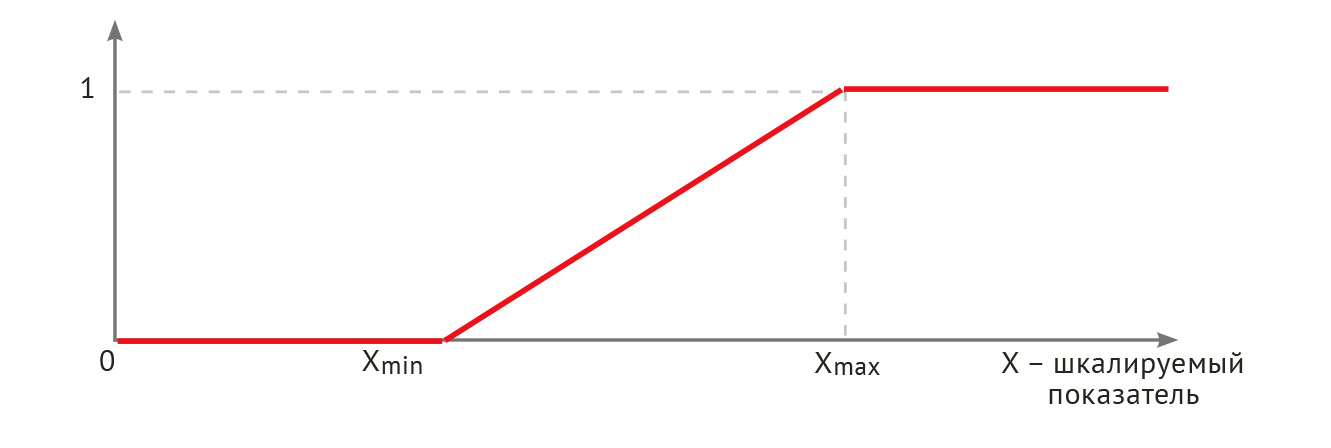
Рис. 1. График линейной одноинтервальной шкалы.

В результате u_i(x_i) переводит шкалы показателей x_i в стандартизированную шкалу 0 ≤ u_i ≤ 1, где чем больше значение u_i, тем лучше. Это позволяет в комплексных и интегральных показателях сравнивать по полезности частные показатели i и j путём определения их весов a_i и a_j.

Для убывающих по полезности показателей (x: v(xmin) > v(x_max)) можно использовать аналогичную функцию:

v(x) = (x_max – x)/(x_max – x_min), 0 ≤ v(x) ≤ 1. (2)

В линейной одноинтервальной шкале базовых параметров два: x_min и x_max. Соответственно, для полного определения шкалы надо задать только эти две точки 2. В этом-то и заключается управленческая проблема — научная и практическая.

Преимущества и недостатки линейной одноинтервальной шкалы. Во-первых, в этой шкале нет планового значения, есть только «провал» x_min и «идеал» x_max. Хотя плановое значение может быть задано внутри этого интервала и его оценка может быть промежуточной, например 0,7 (в этом случае получается частный случай шкалы (X, 100, Y), которую мы рассмотрим ниже). Кроме этого, линейная одноинтервальная шкала не идеальна по двум причинам:

1. Сложно определить крайние значения х_min и х_max. Дело это на 99% субъективное и субъективность выбора значений минимума и максимума, как правило, не получается преодолеть (хотя во второй части цикла я приведу удачный пример).
2. Как известно из курса экономической теории, в общем случае, предельная полезность — это нелинейная функция, скорость роста которой должна убывать, а в нашем случае полезность линейно растёт.

Как бороться с первым недостатком? Общие принципы определения крайних значений следующие. Значение х_max следует выбирать на уровне тактического целевого значения показателя, оно должно быть реально достижимым к окончанию планового периода. Значение х_min должно соответствовать пассивным действиям при неблагоприятной ситуации. Эти значения нелегко определить, но практика показывает, что это можно сделать, по крайней мере, для отдельных показателей. Если стоит задача мотивировать сотрудников, то выбор минимальных и максимальных значений показателя должен быть хорошо обоснован и понятен сотрудникам, иначе есть риск эффекта демотивации.

Демпфировать второй недостаток — нарушение закона предельной полезности в линейной шкале — призвана нелинейная одноинтервальная шкала. Предельная полезность — это дополнительная полезность, которую человек получает от использования ещё одной единицы блага. Говоря математическим языком — это производная функции общей полезности по единицам блага. Закон убывающей предельной полезности заключается в том, что с ростом потребления общая полезность, получаемая потребителем, возрастает, но скорость роста замедляется. По мере постепенного насыщения потребностей субъекта полезность блага для него падает. Предельная полезность повышается при недостатке блага и понижается при его избытке. То есть закон убывающей предельной полезности на математическом языке гласит, что функция общей полезности возрастает и выпукла вверх.

Самая распространённая методика построения нелинейных одноинтервальных функций полезности, известная ещё с середины прошлого века, состоит в нахождении точки интервала х_0,5, где ценность средняя: u(х_0,5) = 0,5. И эта точка лежит не посередине отрезка (х_min, х_max), принцип убывания предельной полезности говорит, что эта точка находится левее середины отрезка (х_min, х_max). Если экспертно оценить точку х_0,5, то специальный математический аппарат позволяет подобрать нелинейную функцию, описывающую функцию ценности по трём точкам: х_min, х_0,5, х_max.

Однако, воспользоваться этим методом и построить нелинейную одноинтервальную шкалу оценки на практике мне пока не удалось. Причина в том, что эксперты не понимали, что от них требуется. Например, в одной из попыток главный эксперт дал значение х_0,5 (делящее ценность выручки пополам) ближе к лучшему значению. То есть фактически он предполагал вогнутость функции ценности, чего не может быть. Это свидетельствует о том, что вопросы о соотношении полезностей, задаваемые лицам, принимающим решения, находятся вне их понимания и потому надёжность получаемых функций невелика. Поэтому, как правило, приходится ограничиваться линейной функцией ценности для каждого показателя.

Шкала Харрингтона

Шкала Харрингтона — это многоинтервальная дискретная вербально-числовая шкала, состоящая из пяти интервалов единичного отрезка, характеризующих степень приближения к некоторому идеалу:

• очень высокая (0,8 — 1,0);
• высокая (0,63 — 0,8);
• средняя (0,37 — 0,63);
• низкая (0,2 — 0,37);
• очень низкая (0 — 0,2).

Численные значения градаций шкалы Харрингтона получены на основе анализа и обработки большого массива статистических экспертных данных. Она переводит качественные оценки в количественные в интервале от 0 до 1 на основе статистической обработки психологических особенностей человека (психометрическая шкала). Шкала Харрингтона универсальна и может использоваться для оценки различных качественных показателей.

Исходная психометрическая шкала для построения шкалы Харрингтона — это шкала Ликерта. Обычно в ней выделяют пять градаций, например:

• полностью не согласен;
• не согласен;
• где-то посередине;
• согласен;
• полностью согласен.

Шкала Ликерта порядковая, а Харрингтон перевел её в количественную, задающую ширину интервалов (интервальную шкалу). Шкала Ликерта широко применяется в социологии, гораздо реже шкалу Ликерта используют в маркетинговых и экономических исследованиях. В практике управления эта шкала применяется редко, ибо остаётся непонятной для менеджеров.

* * *

В следующей части цикла я расскажу о шкалах показателей, имеющих плановое значение.

Комментарии 0