Управленческие шкалы.

Шкала без ограничения на перевыполнение плана

Шкала (Х, 100, бесконечность) — это шкала без ограничения на перевыполнение плана (рис. 7). По сути, она является частным случаем шкалы (Х, 100, Y).

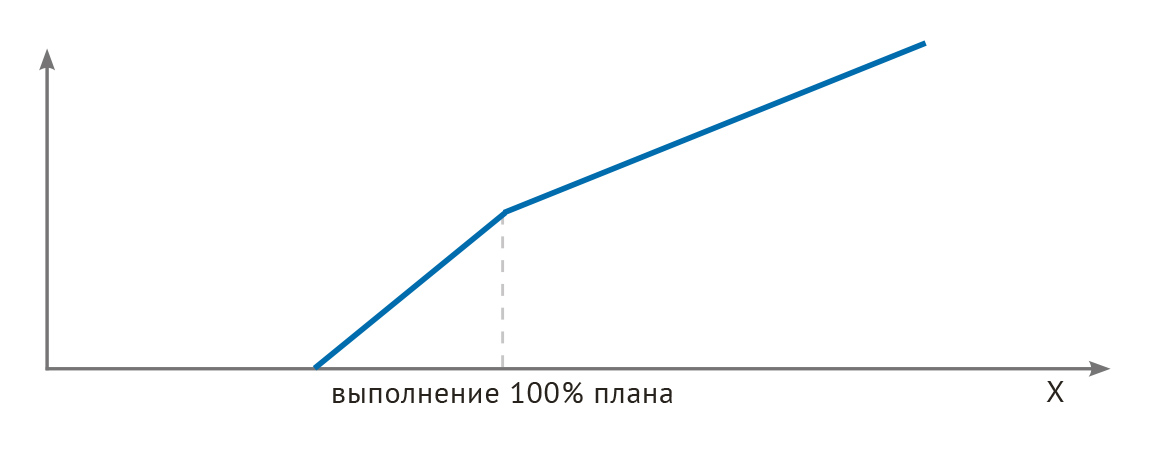
Рис. 7. Шкала без ограничения на перевыполнение плана (Х, 100, бесконечность).

Шкалы со штрафами

Кусочно-линейная двухинтервальная шкала со штрафом. Это тоже развитие двухинтервальной шкалы (Х, 100, Y). Логика развития проста: критическое невыполнение плана должно штрафоваться. Вариантов здесь несколько и они отличаются предельным размером штрафа (рис. 8). Например, предельный штраф может быть установлен равным премии за стопроцентное выполнение плана. В общем случае это так называемый обнуляющий штраф, который  распространяется на оценку выполнения всех плановых значений различных показателей. Например, в компаниях с государственным участием оборонного назначения, если не выполнен государственный оборонный заказ, то оценка всех показателей деятельности компании обнуляется и премий руководству не будет.

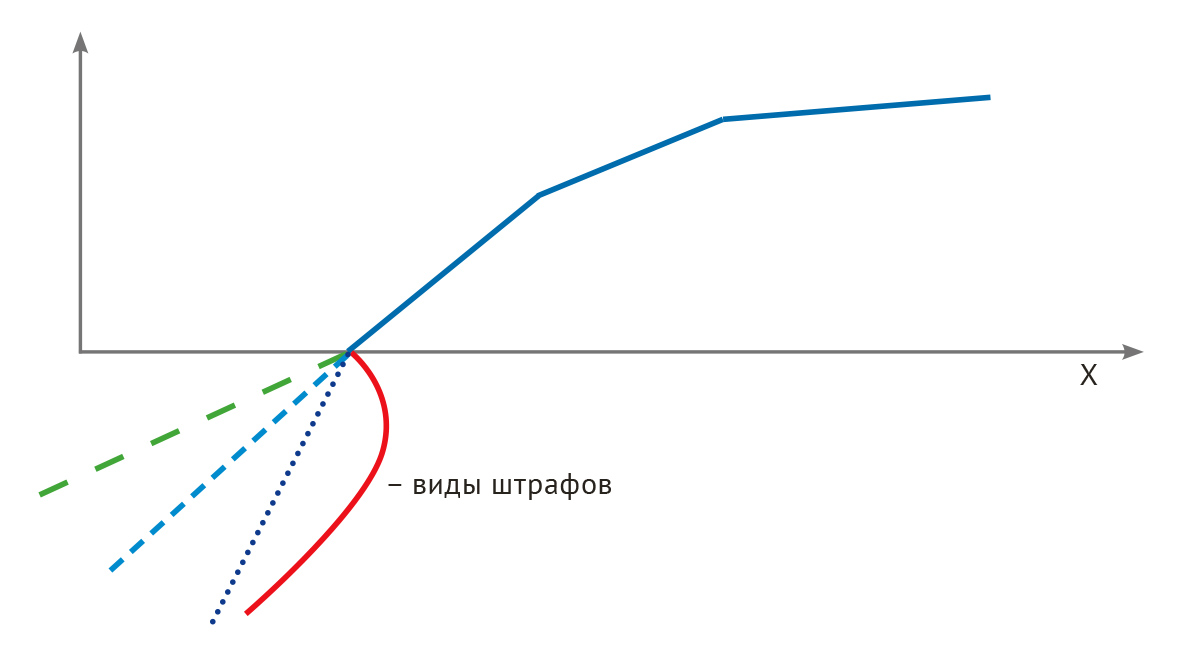
Рис. 8. Кусочно-линейная двухинтервальная шкала со штрафом (несколько вариантов).

Линейная одноинтервальная шкала со штрафом — это шкала, в которой функция полезности линейно возрастает, но не от планового значения, а от некоторого минимального, меньшего планового (рис. 9).

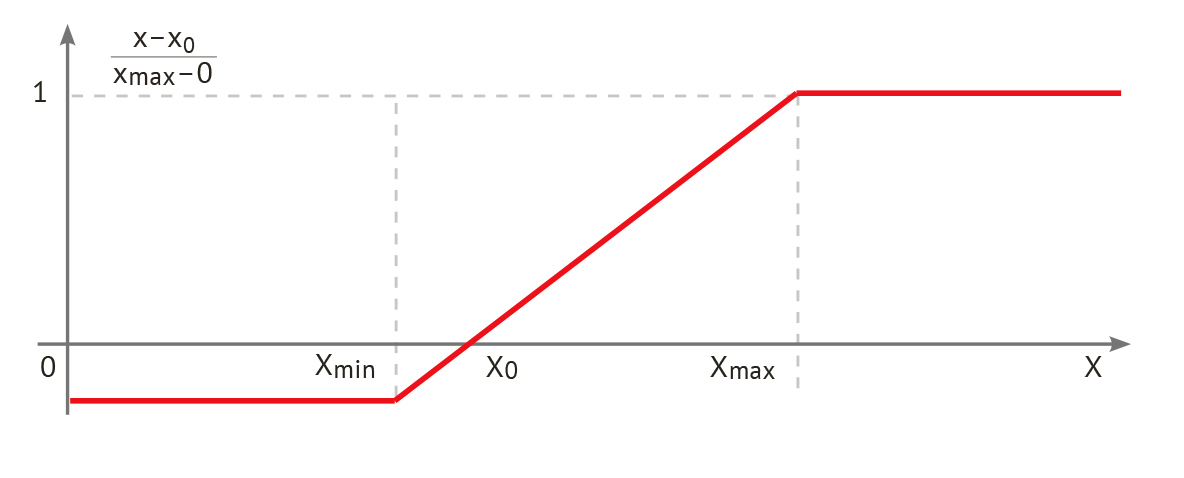
Рис. 9. Линейная одноинтервальная шкала со штрафом.

Двухинтервальная кусочная шкала с нелинейным участком

Как ясно из названия, это двухинтервальная кусочная шкала, которая нелинейна на одном участке (рис. 10). Такая шкала используется для стимулирования приращений, значимость которых изменяется по мере достижения цели. Часто используется такой подход: больше стимулируются предельные приросты результата в ситуации более близкой к напряжённому плану (значение 1 на графике) или идеалу (значение 2). В частности, на нелинейном участке используется квадратичная функция для абсолютных показателей или квадратный корень для процентных показателей.

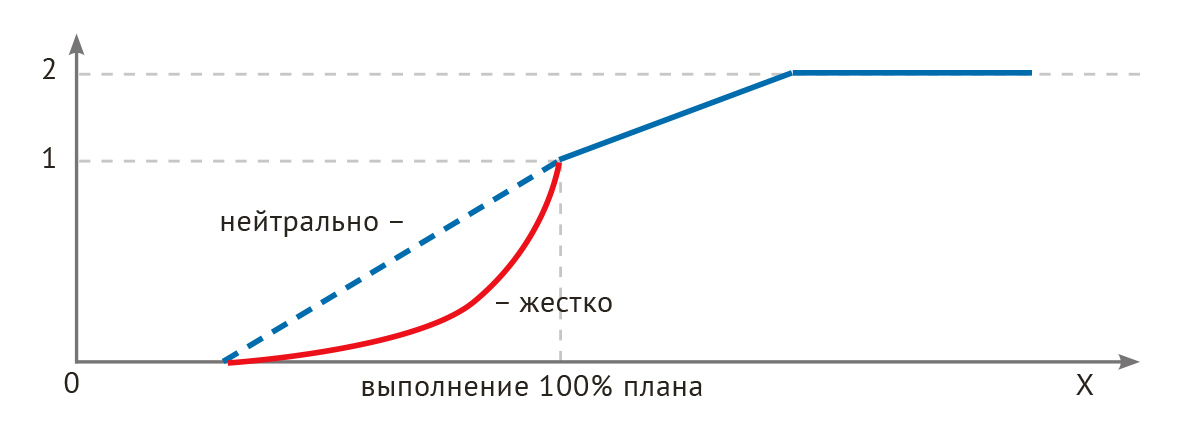
Рис. 10. Шкала с большим стимулированием предельных приростов результата в ситуации близкой к напряжённому плану.

Особые варианты двухинтервальных кусочно-линейных шкал

Рассмотрим частные случаи двухинтервальных кусочно-линейных шкал, используемых для оценки показателей прибыли.

Шкала «нулевая прибыль — целевая (плановая) прибыль — предельно возможная прибыль» (рис. 11). Это вариант шкалы (Х, 100, Y), который используется как для мотивации достижения планового значения прибыли, так и для его перевыполнения. В чем её прелесть? Во-первых, есть «естественная точка» Х — точка безубыточности. Во-вторых, зачастую есть основания для планирования целевой прибыли. Однако, таких же оснований для определения «предельно возможной прибыли», как правило, нет.

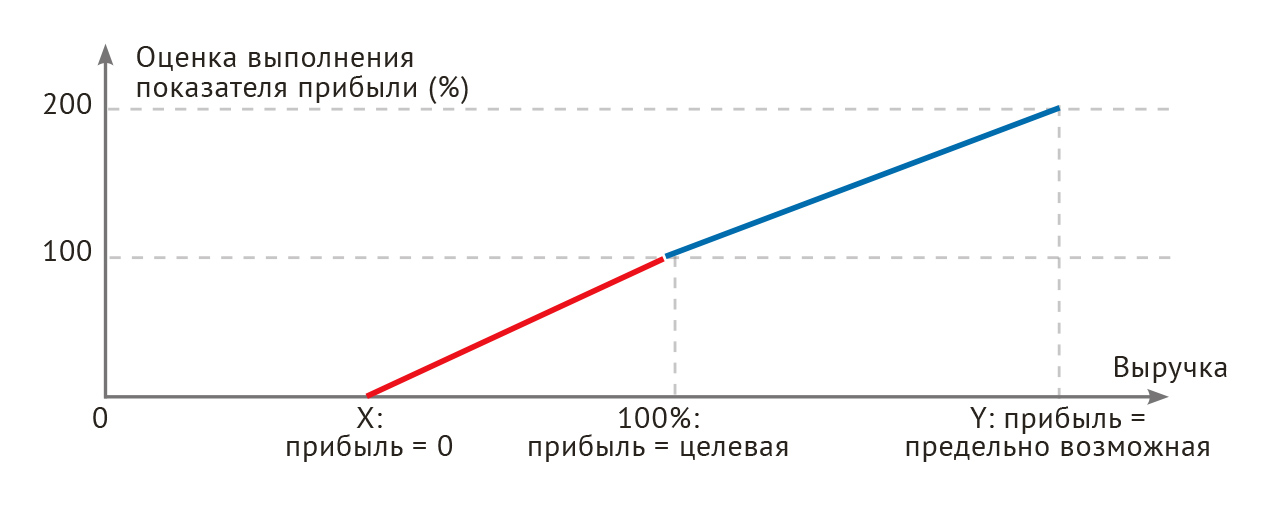
Рис. 11. Шкала «нулевая прибыль — целевая (плановая) прибыль — предельно возможная прибыль».

Шкала «нулевая прибыль — целевая (плановая) прибыль — бесконечность (нет ограничения)». Если оснований для определения «предельно возможной прибыли» нет, то логичнее выглядит эта шкала. Однако существует ограничение: шкалы, основанные на классическом показателе прибыли, пригодны для компании в целом, но для бизнес-направления, продукта или центра прибыли надо перейти к родственным шкалам, основанным на маржинальных показателях.

Шкала «нулевая маржинальная прибыль — целевая маржинальная прибыль — предельное перевыполнение цели (или бесконечность)» (рис. 12). Напомним, что маржинальная прибыль есть выручка минус переменные затраты, то есть затраты, которые изменяются при изменении объёма производства 2. Шкала, оценивающая маржинальную прибыль, корректна для продуктового направления или отдельного продукта.

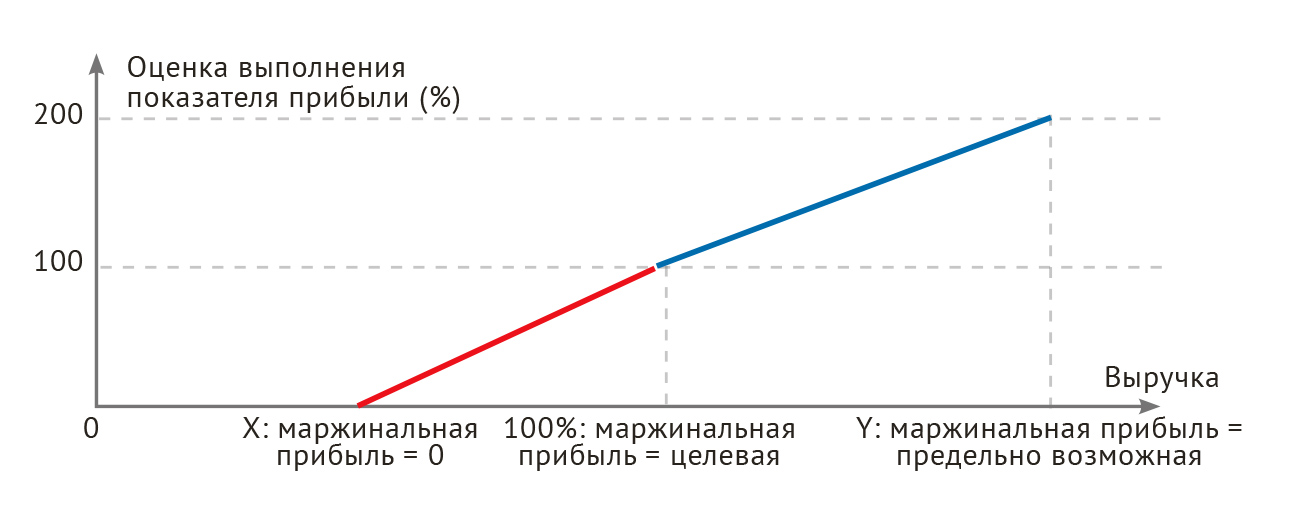
Рис. 12. Шкала «нулевая маржинальная прибыль — целевая маржинальная прибыль — предельно возможная маржинальная прибыль».

Шкала «нулевой маржинальный доход — целевой маржинальный доход — предельное перевыполнение цели (или бесконечность)». На большинстве российских предприятий не выделяют переменных и постоянных затрат, а пользуются прямыми и косвенными затратами 3. Напомню, что прямые затраты связаны с производством определённого вида продукции и могут быть на основании данных первичных документов прямо и непосредственно отнесены на её себестоимость. Если предприятие выделяет прямые и косвенные затраты, стоит использовать шкалу, оценивающую маржинальный доход, который является разницей между выручкой и прямыми затратами на производство продукта. Такая шкала корректна для любого направления, центра прибыли или отдельного типа продукта. Но для управления продуктовым направлением или деятельностью вокруг отдельного продукта она менее точна.

Семейство шкал ABCD или трёхинтервальные шкалы

Кусочно-линейная многоинтервальная шкала — это шкала, в которой функция полезности линейно возрастает, но этот рост различен на разных участках. Рассмотрим, например, семейство шкал ABCD для оценки выручки и прибыли маржинально неубыточных центров прибыли (рис. 13). Измерение и оценка в такой шкале непрерывны, используются в основном линейные отрезки, хотя отдельные участки могут и отличаться от линейных 4.

Оси:

• «измерение» (первичный показатель) откладывают по оси абсцисс, выручка (или прибыль) — это основной вариант оси «измерение»;
• «оценка» (вторичный, оценочный первичный показатель) откладывают по оси ординат — она задаётся в процентах от мультипликатора вознаграждения (200% для шкалы (80, 100, 130)) по результатам выполнения плана по выручке (за план начисляется 100%, 1 или 100 баллов).

Смысл точек на оси «измерение» (при условии, что A < B  < C < D):

• А — точка безубыточности собственных затрат центра прибыли (точка покрытия суммы прямых постоянных и переменных затрат центра прибыли) без распределения общеадминистративных затрат на центр прибыли;
• В — точка безубыточности полных затрат центра прибыли, равных собственным (прямым постоянным и переменным) плюс распределённые общеадминистративные затраты на центр прибыли;
• С — точка целевой прибыли центра прибыли, на практике чаще всего выступает в форме плана по выручке (например, + 20% к полным затратам);
• D — точка, ограничивающая сверху вознаграждение (обычно, если вознаграждение за С взять за 100, то вознаграждение за D берут за 200); отметим что, D = бесконечность — вполне возможная ситуация: она подразумевает неограниченный рост оценки с увеличением выручки.

Обратите внимание, что точки А, В, С — это значения выручки центра прибыли. Темп роста на интервалах [A, B], [B, C], [C, D] различен. Вариант шкалы ABCD — шкала (А, В, С, бесконечность).

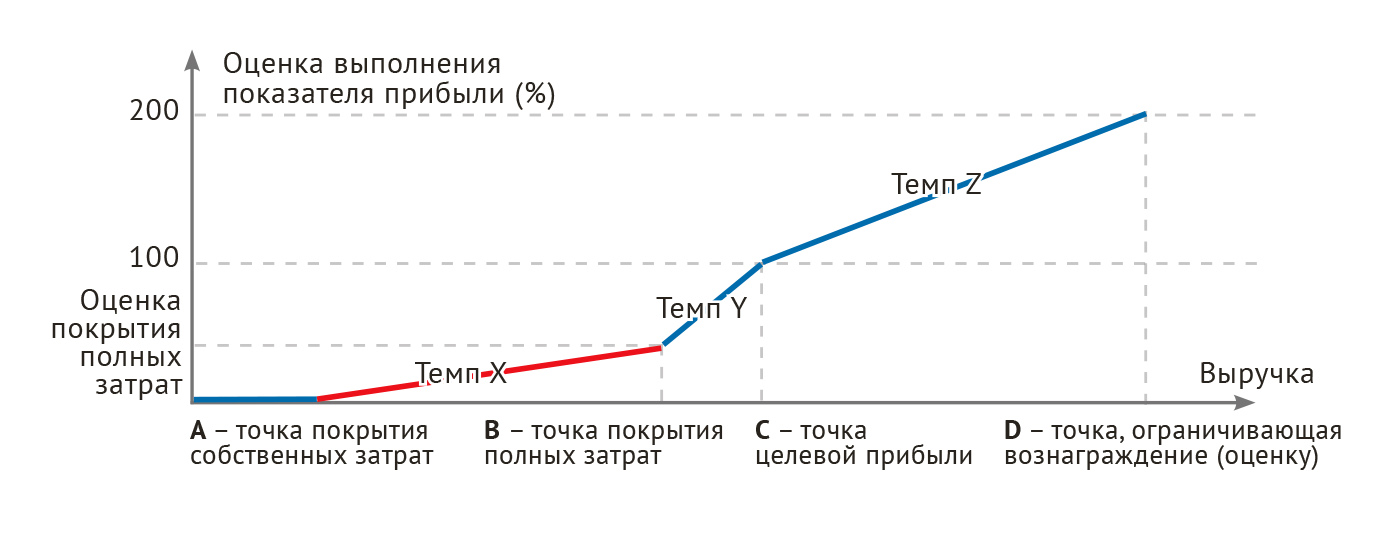
Рис. 13. Шкала ABCD для оценки и мотивации прибыльных центров прибыли.

Преимущества и недостатки кусочно-линейной многоинтервальной шкалы. Главное преимущество — это возможность оценки прибыли через оценку выручки. Ведь, задавая шкалу для оценки выручки, фактически мы оцениваем и прибыль. В результате достаточно одной такой шкалы, чтобы отразить весь тактический финансовый результат. Однако, это верно лишь для маржинально неубыточных центров прибыли. Для маржинально убыточных и маржинально прибыльных ЦФО система оценок должна быть принципиально различной. Для подтверждения этого вспомним, что увеличение выручки для убыточных ЦФО — это плохо, а для прибыльных — хорошо.

Многоинтервальная кусочно-линейная шкала может быть построена на основе показателей, изменяющихся формально от 0 до бесконечности, от 0 до 100%, от минус бесконечности до плюс бесконечности. Однако, у этой шкалы есть и недостатки:

• A и B — точки жёсткие, объективные, жёстко привязаны к конкретной ситуации;
• C и D — произвольно назначаемые субъективные точки, их можно менять при фиксированых А и В.

Можно использовать только три точки, а можно и больше четырёх — всё зависит от настройки модели на конкретный центр прибыли и фирму.

* * *

В следующей части цикла мы опишем шкалы, применяемые для оценки работы и вознаграждения продавцов.

Комментарии 0